5 Rappresentazioni grafiche di base

Illustriamo le principali rappresentazioni grafiche disponibili nella versione base di R. A questo scopo utilizziamo un insieme di dati che riporta le misurazioni della temperatura corporea espresse in gradi centigradi e della frequenza cardiaca espressa in termini di numero di battiti al minuto per maschi e femmine. In particolare, la prima colonna contiene le misurazioni della temperatura corporea, la seconda colonna l’indicazione del genere maschile o femminile codificato rispettivamente con 1 e 2 e la terza colonna le misurazioni della frequenza cardiaca.

Si possono visualizzare le prime osservazioni dei dati con la funzione head

##   temperatura sesso battiti
## 1        35.7     1      70
## 2        35.9     1      71
## 3        36.1     1      74
## 4        36.1     1      80
## 5        36.2     1      73
## 6        36.2     1      75

Per vedere la ripartizione di maschi e femmine si può calcolare la frequenza relativa percentuale delle due modalità della variabile sesso

## 
##   1   2 
## 0.5 0.5

e rappresentare graficamente la variabile sesso con la funzione barplot, che serve per realizzare diagrammi a rettangoli separati, ed è adatta a variabili che sono su scala qualitativa sconnessa o ordinale

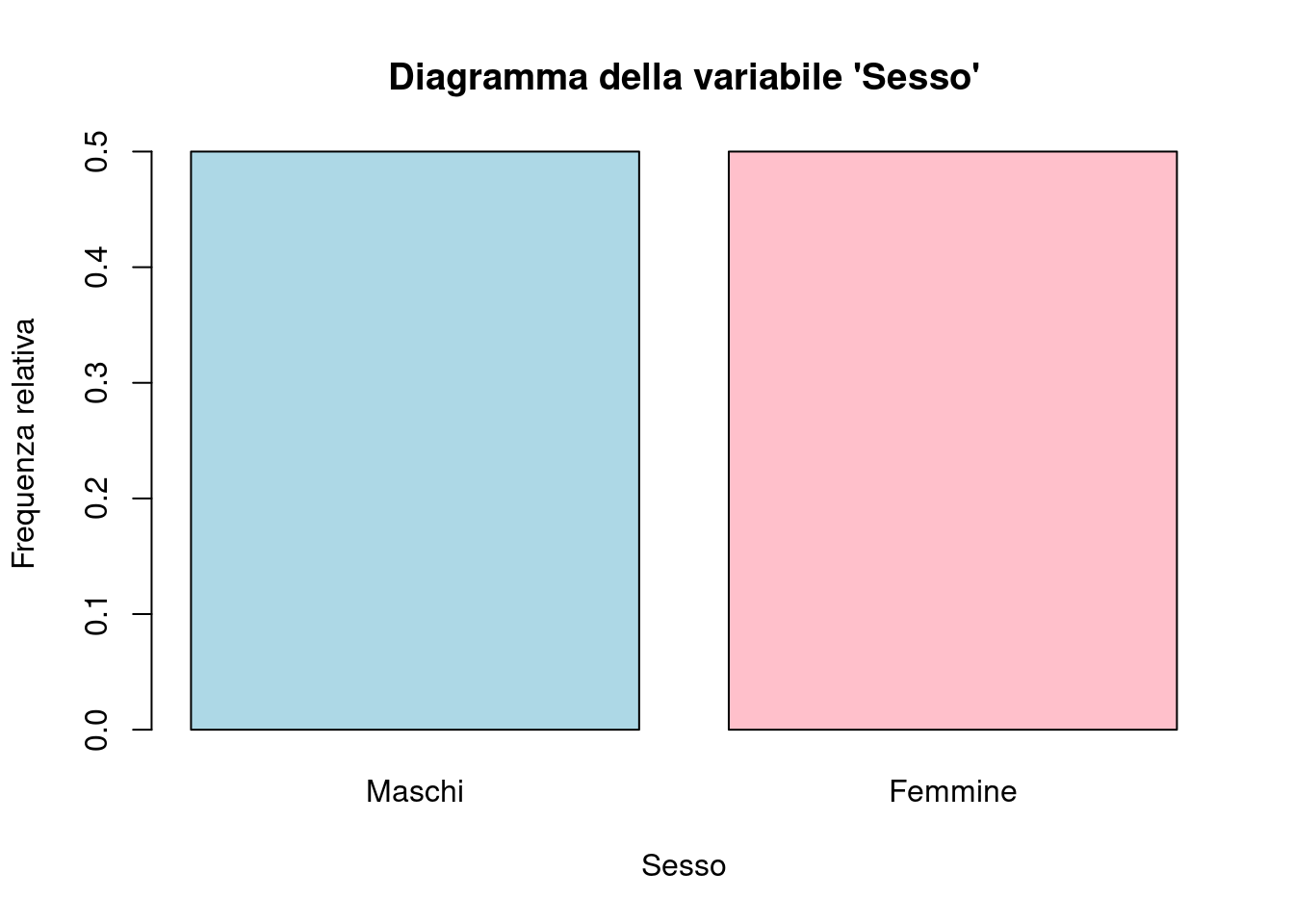
Gli argomenti xlab e ylab sono la descrizione degli “assi”, main è il titolo del grafico, mentre names.arg contiene il nome delle modalità della variabile. Dal grafico si vede che vi è un ugual numero di misurazioni riferite ai maschi e alle femmine.

Si possono creare tre vettori contenenti le tre diverse variabili analizzate,

Per rappresentare graficamente una variabile quantitativa, si può semplicemente utilizzare il grafico ramo-foglia (stem-leaf), attraverso la funzione

## 
##   The decimal point is 1 digit(s) to the left of the |
## 
##   356 | 0
##   358 | 000
##   360 | 000
##   362 | 000000000000
##   364 | 0000000000
##   366 | 0000000000000000000000000
##   368 | 000000000000000000000000000
##   370 | 0000000000000000000000000000
##   372 | 0000000000000
##   374 | 00000
##   376 | 0
##   378 | 0
##   380 | 
##   382 | 0

dove si vede che la classe modale è costituita dalla classe \(37.0 \vdash 37.2\). Una rappresentazione grafica alternativa e forse più usata è l’istogramma (l’istogramma e il diagramma a rettangoli separati sono due rappresentazioni simili dal punto di vista visivo ma ben diverse per costruzione e interpretazione,ne discuteremo nella parte che riguarda la statistica descrittiva)

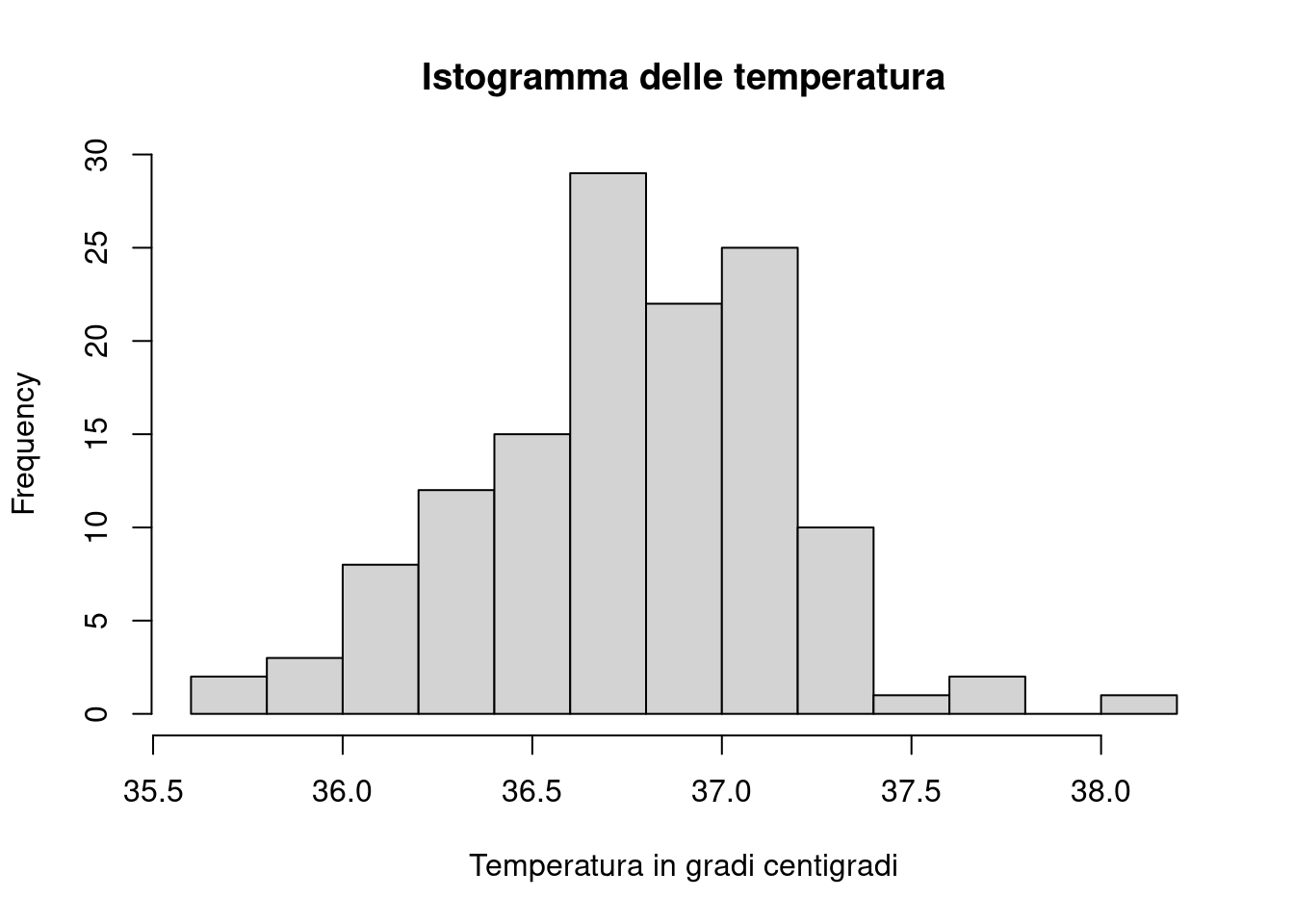
Diversamente dalla funzione barplot nella funzione hist l’area rappresenta la frequenza della classe.

R decide automaticamente il numero di classi, in questo caso ha generato \(13\) classi. Il numero di classi può essere facilmente fissato usando l’argomento breaks

Come si vede dalla figura, aumentare il numero di classi porta ad un maggiore dettaglio. Specificando un vettore di valori nell’argomento breaks definiamo gli estremi delle classi, in questa maniera precisiamo sia l’ampiezza delle classi (che può risultare diversa) sia il numero di classi, inoltre con l’argomento probability=FALSE otteniamo un grafico che usa le frequenze assolute invece delle frequenze relative

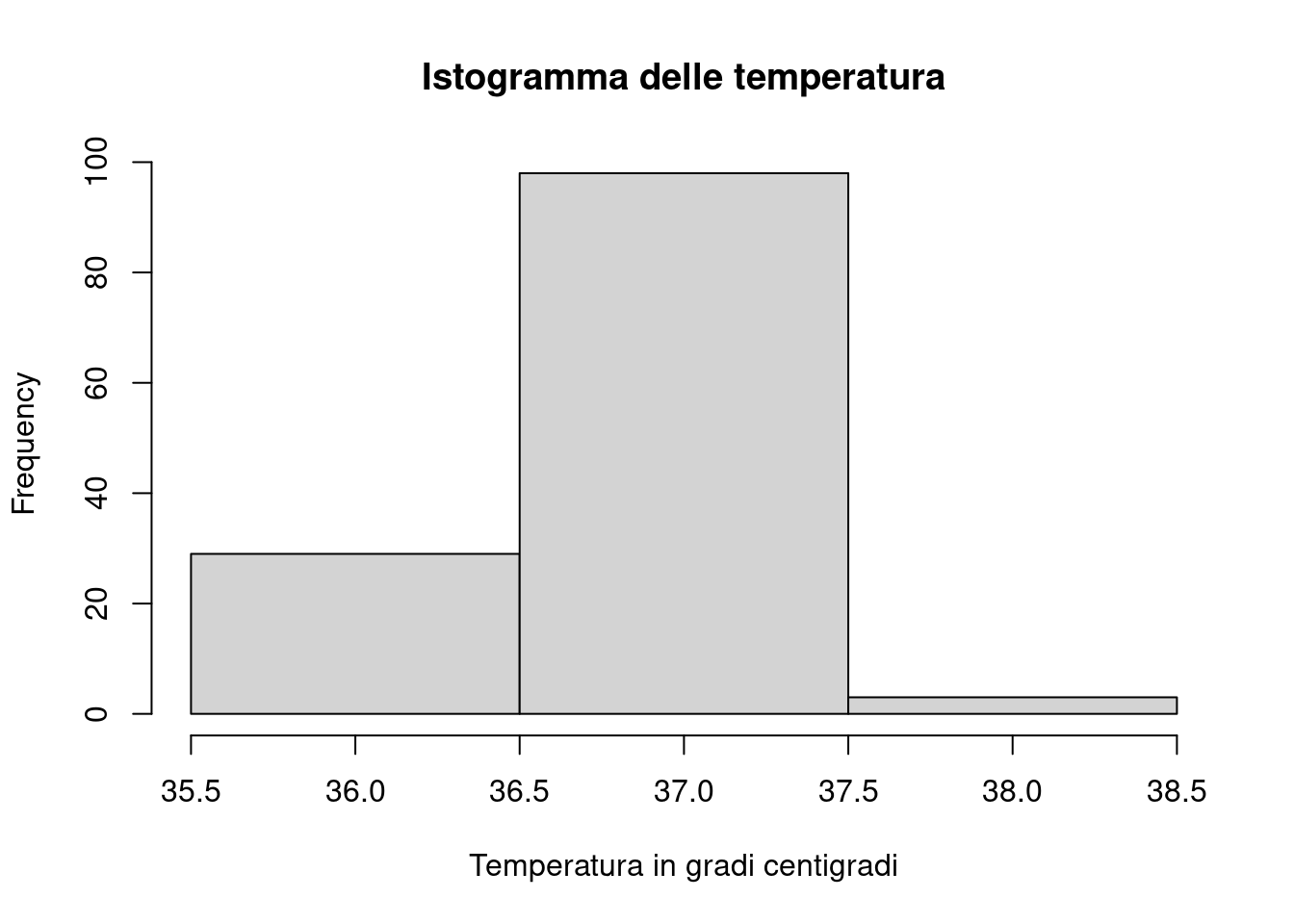
Nella figura abbiamo l’istogramma definito con tre classi. Se usiamo l’argomento plot=FALSE il grafico non verrà presentato nella finestra grafica, questa opzione è utile se vogliamo memorizzare in una variabile le informazioni relative ad un istogramma

## Warning in hist.default(temperatura, breaks = c(35.5, 36.5, 37.5, 38.5), :
## argument 'probability' is not made use of
## List of 6
##  $ breaks  : num [1:4] 35.5 36.5 37.5 38.5
##  $ counts  : int [1:3] 29 98 3
##  $ density : num [1:3] 0.2231 0.7538 0.0231
##  $ mids    : num [1:3] 36 37 38
##  $ xname   : chr "temperatura"
##  $ equidist: logi TRUE
##  - attr(*, "class")= chr "histogram"

In $breaks ci sono gli estremi delle classi, in $counts ci sono le frequenze assolute che cadono all’interno di ogni classe, mentre in $rel.freqs ci sono le frequenze relative, anche se a volte questa variabile non sembra calcolata correttamente, quindi si presti particolare attenzione al suo utilizzo. In $mids sono riportati i valori centrali delle classi.

Può risultare interessante verificare se esiste una differenza tra la distribuzione delle temperature registrate per i maschi e la distribuzione per le femmine. Suddividiamo le misurazioni relative alla temperatura in due vettori distinti:

Usando le funzioni summary e boxplot.stats vediamo se vi sono differenze tra le due distribuzioni. In particolare i valori forniti da boxplot.stats si riferiscono a $stats: l’estremo inferiore del baffo, l’estremo inferiore della scatola, il valore centrale, l’estremo superiore della scatola e l’estremo superiore del baffo; $n: il numero di osservazioni; $out: il valore di tutte le osservazioni che sono al di fuori dei baffi.

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   35.70   36.40   36.70   36.73   37.00   37.50
## $stats
## [1] 35.7 36.4 36.7 37.0 37.5
## 
## $n
## [1] 65
## 
## $conf
## [1] 36.58242 36.81758
## 
## $out
## numeric(0)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   35.80   36.70   36.90   36.89   37.10   38.20
## $stats
## [1] 36.2 36.7 36.9 37.1 37.7
## 
## $n
## [1] 65
## 
## $conf
## [1] 36.82161 36.97839
## 
## $out
## [1] 35.8 35.9 36.0 37.8 38.2

La temperatura delle femmine sembra leggermente superiore a quella dei maschi, ma per decidere quanto questa differenza sia realmente significativa è necessario utilizzare una tecnica che vedremo più avanti basata sulla statistica inferenziale.

Per rappresentare in un diagramma a scatola e baffi le temperature possiamo scrivere

Oppure per ottenere lo stesso risultato possiamo usare la seguente sintassi che risulta equivalente

dove la sintassi temperatura ~ sesso si chiama formula ed è un modo molto generale e potente per descrivere quello che vogliamo fare. Ne riparleremo in dettaglio più avanti. Dal diagramma a baffi si nota come la distribuzione della temperatura corporea delle femmine tenda ad essere più elevata di quella dei maschi. Differenze si possono trovare anche nella dispersione di queste due distribuzioni.

Infine un’ulteriore maniera per verificare se le distribuzioni della temperatura dei maschi e delle femmine sono oppure no le stesse, possiamo usare una rappresentazione basata sui quantili

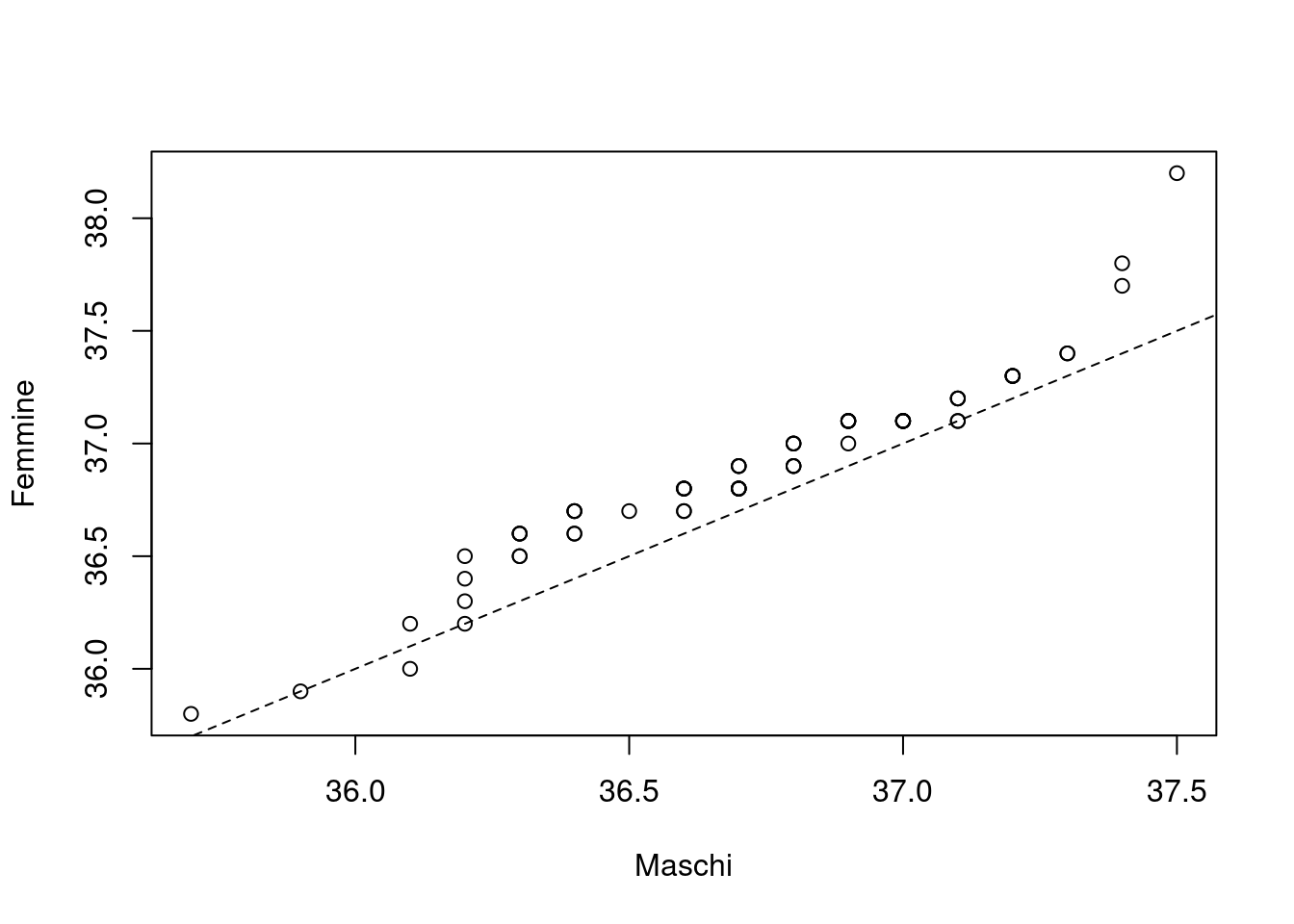
Quando siamo interessati allo studio della relazione tra due variabili quantitative su scala continua, è sempre opportuno rappresentare le osservazioni in un piano cartesiano. In R questo si ottiene facilmente attraverso la funzione plot

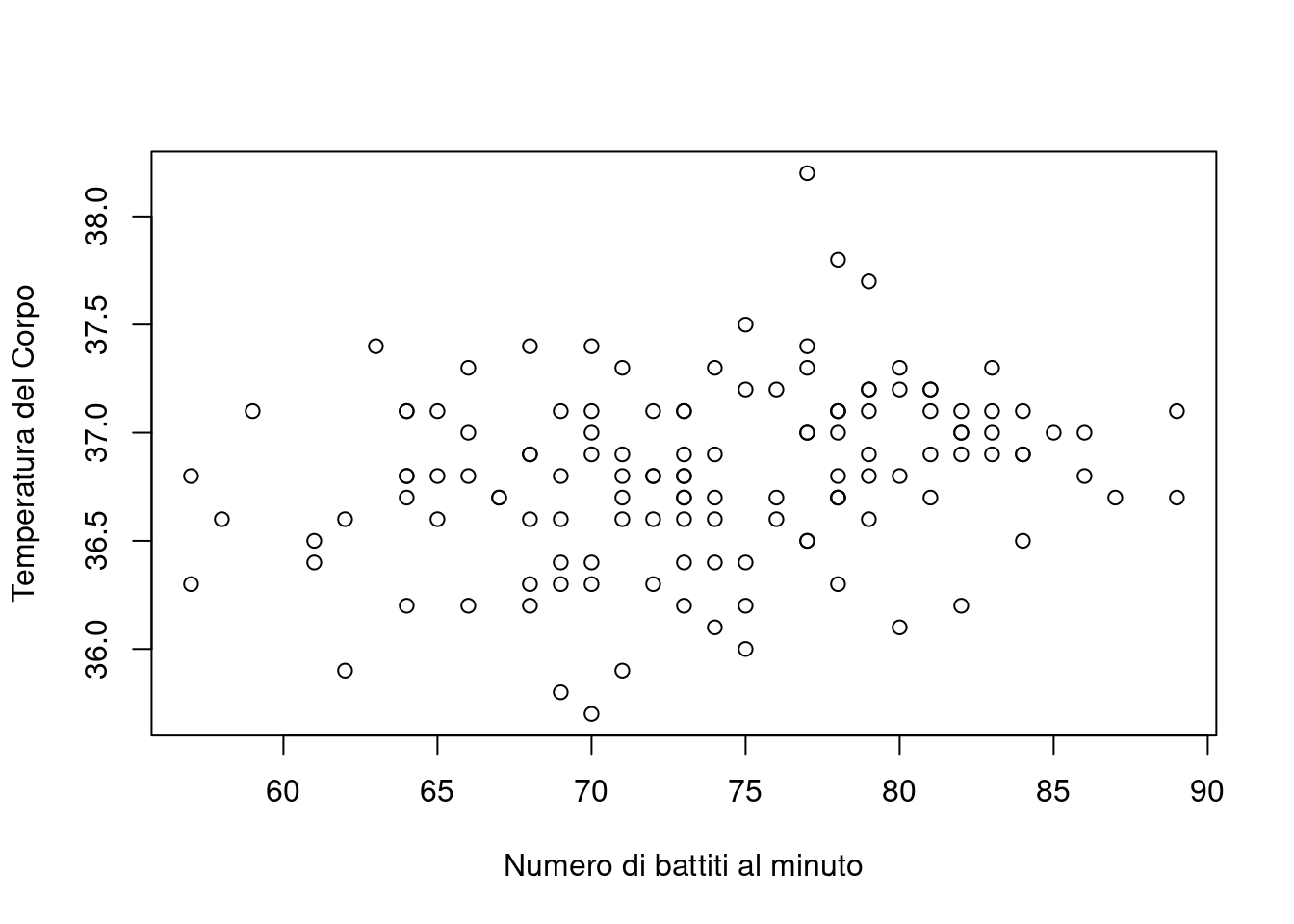
Come si vede dal grafico non sembra esserci una relazione marcata tra la temperatura corporea e il numero di battiti al minuto.

In questo contesto potrebbe essere interessante vedere dove sono collocate le osservazioni che si riferiscono alle femmine rispetto a quelle dei maschi. Per ottenere un grafico di questo genere possiamo scrivere

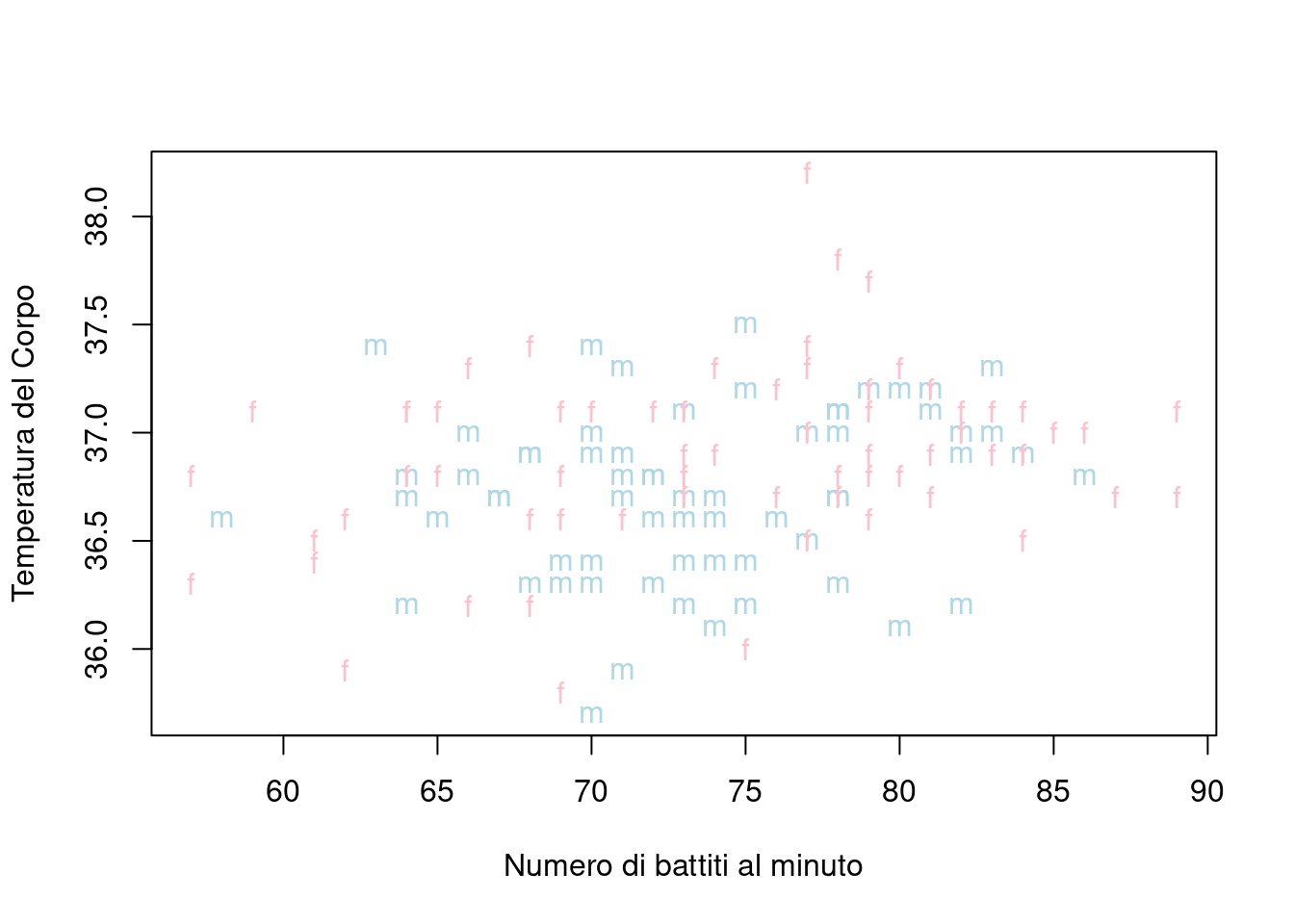
o in maniera più semplice, ma meno elegante,

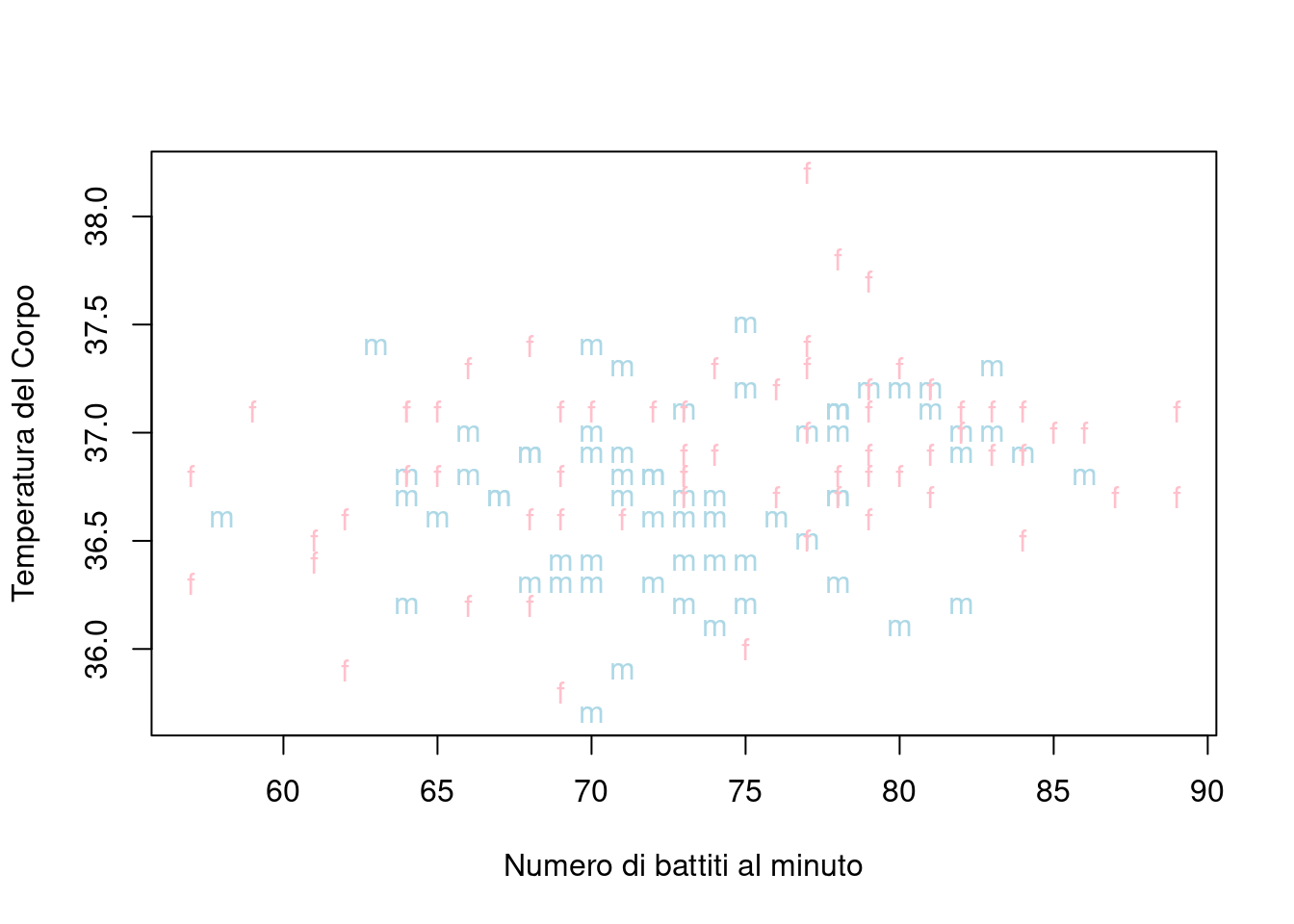
dove prima abbiamo preparato il grafico (si noti l’argomento type="n") e poi con la funzione points abbiamo aggiunti i punti. Dal grafico non si evidenzia una marcata differenza tra le osservazioni riferite alle femmine rispetto a quelle riferite ai maschi.