Outlier-robust estimation of state-space models using a penalised approach

• School of Mathematics and Statistics, University of Sydney, Sydney, Australia [rajan.shankar@sydney.edu.au, garth.tarr@sydney.edu.au]

• Department of Quantitative Economics, Maastricht University, Maastricht, Netherlands [i.wilms@maastrichtuniversity.nl]

• Department of Mathematics, University of Antwerp, Antwerp, Belgium [jakob.raymaekers@uantwerpen.be]

Keywords: state-space model – robustness – regularisation – animal tracking

1 Background

State-space models (SSMs) are a broad class of statistical models for modelling time-varying data. SSMs consist of an observed process (1) and a latent state process (2):

${𝐲}_t$ $=A{𝐱}_t+{𝐯}_t$ (1)

${𝐱}_t$ $=\mathrm{\Phi }{𝐱}_{t-1}+{𝐰}_t,$ (2)

where ${𝐯}_t$ and ${𝐰}_t$ are observational and state disturbances, $\mathrm{\Phi }$ is the state-transition matrix, and $A$ represents how states are transformed into observed measurements.

Practitioners use SSMs to infer the structure and dynamics of the state process based on the data from the observed process. However, when estimating state space models, it is common to assume that ${𝐯}_t$ and ${𝐰}_t$ follow normal distributions. This leads to intrinsically non-robust estimators which can result in poor parameter estimates in the presence of outliers.

There are techniques in the literature, such as that of Duran-Martin et al. [2024], to robustly estimate the states ${𝐱}_t$ assuming that the SSM parameters — usually $\mathrm{\Phi }$ and the variances of ${𝐯}_t$ and ${𝐰}_t$ — are known. Our approach differs from these techniques by focusing on robustly estimating the SSM parameters as well.

2 Method

To robustly fit a SSM in the presence of outliers, we take inspiration from the iterative procedure for outlier detection (IPOD) developed by She and Owen [2011] who apply it to ordinary least squares regression models. They modify the regression model by adding $n$ extra parameters — one for each data point. If any of these parameters are estimated as non-zero, it suggests that the corresponding data point is an outlier. This formulation is known as a mean-shift formulation, and was earlier used by McCann and Welsch [2007]. We alter (1) to obtain a mean-shifted observed process:

$${𝐲}_t=A{𝐱}_t+{𝜸}_t+{𝐯}_t,$$

where ${𝜸}_t$, $t=1,\mathrm{\dots },n$, represent the shift parameters.

Since the model is over-parametrised, we impose sparsity among the ${𝜸}_t$’s to prevent them from all being non-zero. This is achieved by using the hard penalty in the estimation procedure,

The tuning parameter $\lambda$ controls how many data points are flagged as outliers, with smaller values of $\lambda$ corresponding to more outliers. We use information criteria to choose an appropriate value of $\lambda$.

3 Results

We run a simulation study where we simulate data under the first-differenced correlated random walk (DCRW) model [Jonsen et al., 2005]; a type of state-space model commonly used for tracking the position of animals over time. We compare our robust method for fitting state-space models to classical approaches and the method of Crevits and Croux [2019]. Our method shows good performance in identifying outliers, as pictured in the example in Figure 1, and in parameter estimation.

Figure 1: Our robust method applied to a simulated data set of position measurements of a moving object over time (grey points), contaminated with outliers (red points). Our method (orange line) closely recovers the true positions of the object (dashed black line), while detecting most outliers correctly (orange circles).

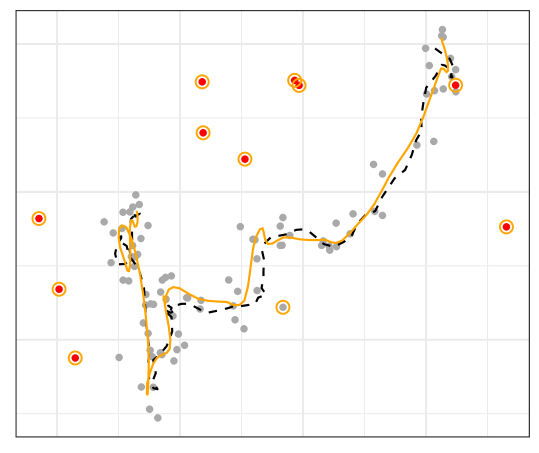
We also apply our method to animal-tracking data, such as polar bear and whale GPS measurements.