Challenges of Cellwise Outliers

• Department of Mathematics, University of Antwerp, Belgium [jakob.raymaekers@uantwerpen.be]

• Section of Statistics and Data Science, KU Leuven, Belgium [peter@rousseeuw.net]

Keywords: Cellwise outliers – covariance – breakdown

1 Cellwise Outliers

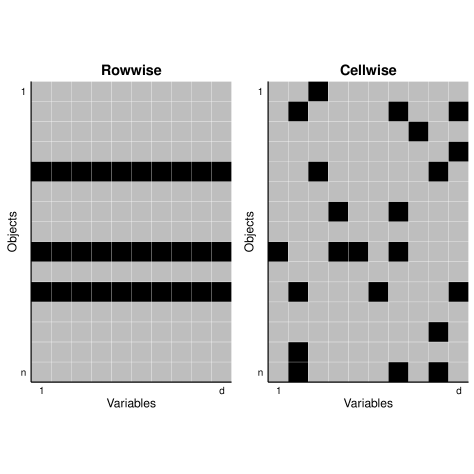
Cellwise outliers were first formalized by Alqallaf et al. [2009] as an alternative to the rowwise paradigm in robust statistics. Conceptually, the two frameworks are easy to understand through the illustration in Figure 1. Under the rowwise paradigm, we aim to limit the influence of individual observations on the estimation of statistical estimands. In the cellwise paradigm, we instead focus on limiting the influence of individual cells in the data matrix. The cellwise approach has two key advantages over the rowwise method. First, even in low-dimensional data, it identifies which specific variables make a case an outlier, providing valuable insight. Second, by discarding only unreliable cells instead of entire observations, more useful data is preserved. In contrast, removing whole rows due to a few outlying values can lead to significant information loss, especially in high-dimensional datasets where just a few outliers can affect every row. The cellwise approach helps prevent this information loss.

Figure 1: Rowwise vs. cellwise contamination

2 Challenges

While the benefits of the cellwise paradigm are evident, it also introduces new and complex challenges. One major issue is that rotating the data can spread cellwise outliers across an entire observation, making orthogonal or affine equivariance not only unnecessary but potentially harmful. This necessitates rethinking statistical methods such as covariance estimation, principal component analysis, and regression. Another second challenge is that outlying cells are not always marginally extreme, meaning that detecting them requires considering the true dependencies within the data. However, estimating these dependencies is difficult when the data already contains cellwise outliers, creating a circular problem that calls for innovative solutions. Finally, since any combination of cells within an observation may be outlying, the number of possible outlier patterns grows exponentially with the dimension. This poses significant computational challenges that require efficient detection and estimation techniques.

Several proposals have been made to deal with cellwise outliers in a variety of settings. These settings include outlier detection, covariance estimation, regression and principal component analysis. While several of these proposals work very well in certain settings, many of them remain hard to understand from a theoretical perspective and have been mainly tested in relatively benign scenarios of cellwise outliers. To contribute to an explanation for this first fact, we illustrate how seemingly natural properties of estimators are incompatible with cellwise robustness when quantified through a cellwise breakdown value. This is the case for the estimation of location, covariance and regression. Nevertheless, we illustrate that it is indeed possible to develop estimators with nontrivial cellwise breakdown values such as the recently introduced cellwise MCD estimator Raymaekers and Rousseeuw [2023]. Despite the progress made so far, the issue of cellwise outliers is far from solved. We discuss pathways forward, and investigate the relation with related issues such as handling data with heavy tails.